Compilers
compilers
Read a source file, and write the output to another file.
Does two things, analysis and synthesis.
- Analysis is basically checking of correctness
- Synthesis is basically generation of the deets from the Intermediate Repr.
Lexing and Parsing
For getting the source code into a digestable, abstract way, you need to have a method of getting the tokens from them. The best way to do it is to use a finite state machine that gives you a token for everything.
So the parser takes the tokens one after the other and matches them with the grammar and the lexer keeps giving the parser once it matches them.
Lexing
It returns two things, an identifier for the token it just read and possibly some sort of value for it.
We use flex for this. It takes multiple regex rules and for each regex it returns a token and its value.
For each rule, it matches tokens based on the Aho-Corasick algorithm. This is basically a preprocessing table for multiple words, similar to KMP algorithm.
vector<int> jump(const string &s) {
int len = 0;
vector<int> v(s.size());
v[0] = 0;
for (int i = 1; i < s.size(); i++) {
if (s[len] == s[i]) {
len++;
v[i] = len;
}
else if (len != 0) {
len = v[len - 1]; // check the previous smaller prefixes of the length
// matched
i--; // we don't want to incrememt without it matching
} else {
v[i] = 0; // Can't be matched, has to be zero
}
}
return v;
}
vector<int> kmp(const string &text, const string &pattern) {
vector<int> jumps = jump(pattern);
vector<int> result;
int text_idx = 0, pat_idx = 0;
while (text.size() - text_idx >= pattern.size() - pat_idx) {
if (text[text_idx] == pattern[pat_idx]) {
pat_idx++; text_idx++;
}
if (pat_idx == pattern.size()) {
result.push_back(text_idx - pat_idx + 1);
pat_idx = jumps[pat_idx - 1];
}
else if (text_idx < text.size() && text[text_idx] != pattern[pat_idx]) {
if (pat_idx) {
pat_idx = jumps[pat_idx - 1];
} else {
text_idx++;
}
}
}
return result;
}
To show that it's linear time, if the increment does not happen for some k iterations, we have already matched the length of atleast k of the pattern and then moved to this spot in the pattern and text. Therefore, it can only do at most ~ 2k iterations for a segment of length k. Hence it is linear in time.
This matches a pattern in a text. We can extend this idea to a DFA for multiple words and transitions based on the input character to achieve what's called as the Aho Corasick automaton.
Usually the longest match is picked. This is also true in (f)lex. In case two of the regexes have the same length, the one above gets matched.
All of this was for theoretical discussion based on string matching. Actual matching is done based on regex rules. There is a conversion from the regex to a DFA using a syntax tree.
We first make the syntax tree of the regex followed by a meta symbol (in
this case #).

We also assign a number to each of the leaves.
- firstpos is the set of positions where the current node's subtree would
start. For
*it will be the same as its child, for concat it'll be the lesser of the two. For or node it will be the union of the two. For concat if the first one can null then it's a union. - lastpos is where they end. Rules are the same. For concat if the second one is nullable then it's a union.
- followpos is the number that would immediately follow the token
represented by the current node. If
aandbare concatenated, then firstpos ofbis the followpos for lastpos ofa. For star node it's the firstpos of the same node. For or node you need to go up.
Now the DFA transitions are as follows:
- Take the root and mark its firstpos as the unmarked state
- While there is an unmarked state
s, mark the states. - For each leaf symbol
a(the input letter in the regex) ins, mark a transition fromsto the union of followpos(p) wherepare the leaf nodes corresponding toa. So if the stateshas firstpos 123, with 1 and 3 beinga, then transition on readingato \(\bigcup followpos(p)\) where p is 1 and 3 in this case
Parsing
There are many kinds of parsers. All of them are supposed to take a Context Free Grammar (or rather, a restriction on it) and recognise programs that conform to it.
A CFG has a set of terminals called tokens. These are what form the bottom rung of the CFG rules.
These compose in a certain way to form rules called productions. A non-terminal is any other token that is not a terminal (i.e. not returned by the lexer) and is a particular order of other terminals or non-terminals in a specified order.
list -> list + digit | list - digit | digit digit -> 0 | 1 | 2 | ... | 9
A production is for a non-terminal if it is on the LHS of the rule, also known as the head. The RHS of the same rule is called the body of the production. A start-symbol is one which is where the parsing starts. A string is said to be derived from a grammar if we can make replacements in the start symbol many times by replacing a non-terminal with the body of the non-terminal's production.
A parse-tree is what is formed when you apply the production rule substitutions to derive a string. Needless to say, there can be multiple parse trees for a single string if the grammar allows it. Such grammars are called ambiguous.
- Precedence and Associativity
This can be encoded in the grammar itself. It could lead to either shift-reduce or reduce-reduce conflicts in the parser. The latter must be avoided at all costs unless you're using a glr parser. The former is still ok on most occasions. If the grammar is ambiguous, then use
%precedencein yacc to specify the precedence order.Once again, even when there's no precedence conflict, you can have associativity problems. You can specify
%leftor%right(eg, equality of variables) for either of the two.If you want left associativity, write left-recursive grammar. Else write right-recursive grammar.
- Sentential forms
At each step in derivation of the string, we make two choices.
- First is to choose which non-terminal in the current string to substitute.
- Second is to choose the production to replace it with.
Two common formats are leftmost and rightmost. Thus, we talk of left sentential and right sentential forms. Rightmost are also called canonical derivations.
- Left Recursion
\(A \xrightarrow{\text{+}} A\alpha\) is what a left recursion is. Top down cannot handle left recursion. There is a generic method to convert left recursion to right recursion.
\begin{gather} A\rightarrow A\alpha_1 | A \alpha_2 |... | \beta_1 | ... | \beta_n \\ A \rightarrow \beta_1 B | ... | \beta_n B \\ B \rightarrow \alpha_1 B | ... | \alpha_m B | \epsilon \end{gather}Algorithm:
- arrange non-terminals in some order \(A_1\) … \(A_n\)
- for \(i = 1\) to \(n\)
- for \(j = 1\) to \(i - 1\)
- replace \(A_i \rightarrow A_j\alpha\) by the rules mentioned above where \(A_i \rightarrow \alpha_1 | ... | \alpha_k\) are current \(A_j\) productions
- eliminate immediate left recursion in \(A_i\) productions.
- for \(j = 1\) to \(i - 1\)
- Left factoring
Bunch common terms on the left side till you only have a single alternative of that kind.
\begin{gather} A\rightarrow \alpha\beta_1 | \alpha\beta_2\\ A\rightarrow \alpha A'\\ A'\rightarrow \beta_1|\beta_2 \end{gather}
Top Down Parsing
- Do a DFS in the parse tree (preorder)
- Find the leftmost derivation at each instant
- Generally does recursive descent which backtracks
Special case is LL(k) which does predictive parsing based on a parse table.
for each production in \(A \rightarrow X_1...X_k\)
- for \(i = 1\) to \(k\)
- if \(X_i\) is a nonterminal call corresponding function
- else if \(X_i\) is the next symbol advance input
- else go back one token (yyless) and break
- if \(A\) matches break;
- else current input position is saved
- for \(i = 1\) to \(k\)
First and Follow sets
- Parsing is aided by FIRST and FOLLOW sets which allow the parser to choose which production to apply.
- First \(\alpha\) is the set of terminals that begin strings when derived from \(\alpha\)
- If \(\alpha \xrightarrow{\text{*}} \epsilon\) , that is also there in the first set
- Follow is the set of terminals that can appear to the right of \(\alpha\)
- If \(S \xrightarrow{\text{*}} \alpha A \beta B\) then follow of \(A\) contains \(\beta\)
- If \(S \xrightarrow{\text{*}} \alpha A B \beta\) then follow of \(A\) contains First \(B\)
- If \(B\) also has \(\epsilon\) in its first, then follow of \(A\) also contains \(\beta\)
- If \(S \xrightarrow{\text{*}} \alpha A\) then follow of \(A\) contains follow of \(S\)
- \(S \xrightarrow{\text{*}} AB\) and \(B\) is nullable then follow of \(A\) contains follow of \(S\)
- Predictive parsing table for LL(1)
- for each production \(A \rightarrow \alpha\)
- for each terminal \(a\) in FIRST \(\alpha\) Table[\(A\)][\(a\)].add(\(A \rightarrow \alpha\))
- if \(\epsilon\) in FIRST \(\alpha\)
- for each terminal \(b\) in FOLLOW \(A\) Table[\(A\)][\(b\)].add(\(A\rightarrow \alpha\))
- if
$is in FOLLOW \(A\) Table[\(A\)][$].add(\(A\rightarrow \alpha\))
Now if a cell is empty after this then it's an error
- for each production \(A \rightarrow \alpha\)
- Conflicts due to the above
- FIRST FIRST (can be solved by left factoring)
- FIRST FOLLOW (combine terms on left so that decision is deferred, basically left factor) In this case however it is an instance of some sort of left recursion.
Bottom Up parsing
Reverse derivation happens from rightmost. Basically, we have the tokens and we combine or reduce them to non-terminals. Hence called LR parsing
A handle is a substring of the production that can be reduced into a non-terminal. This will always be at the top of the stack.
- Shift reduce conflicts appear when the handled can be reduced and another token shifted can also lead to a new reduction. Basically the tail of a production is also a reduction.
- Reduce reduce happens when two different lengths of the top can be reduced to something.
Simple LR or SLR
Shift and reduce, what else do I even say? Every token can be associated with a semantic value, which is like an action in Bison.
Shift reduce decisions are made by generating a set of states that keeps track of where we are in the rule.
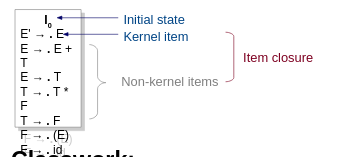
This is how we start.
If [A → α . X β] is in itemset I, then GOTO(I, X) is the closure of the itemset [A → α X . β]. For instance, GOTO(I0, E) is {E' → E ., E → E . + T}.
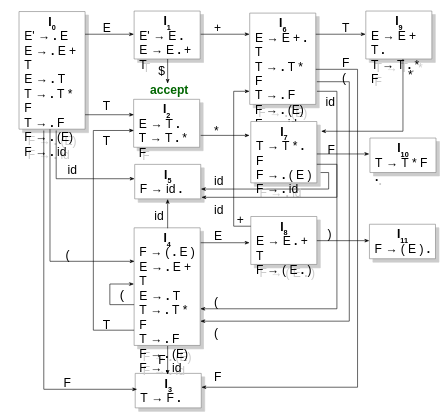
Depending on what we will encounter next, the automaton transitions.
How is the actual parsing done? We start with the initial state I0. We encounter a terminal and then go to the corresponding state in the automaton. Over there we see that the next token we got from the lexer either has a rule going from the current state to another state (shift), or is in the FOLLOW of the topmost token currently. This is checked via the dot in the states.
Shift-reduce happens when there is a transition from one state on encountering a term and it is also there in the follow of the same term for that state.
Reduce-reduce happens when you can go back to different states while reducing and more than one of them contribute to the same token in the follow of the current state.
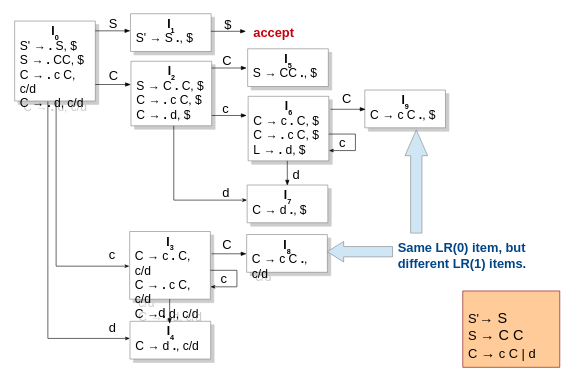
Canonical LR or CLR
Parse with lookahead when creating the automaton. This allows for more precise parsing and lets you write more ambiguous grammar that lets you get better results and cleaner results or some shit like that.
Syntax Directed Translation
This is the actions and attributes that we associate with the derivations/reductions happening during the parsing stage.
Types of attributes:
- Inherited: It is inherited from the parent node or the sibling nodes in the AST. Eg: scoping.
- Synthesized: It is taken from the children nodes of the AST. Eg: most of the parsing constructs.
If only synthesized attributes and actions are there, then any of the bottom-up parsers would work, eg. post-order traversal. There is a dependency graph of how that flows. However, regardless of the types of actions, there must not be a circular dependency in it.
Only using synthesized attributes is called S-attributed SDT. In most situations, however, it is too strict. We can allow attributes to flow from the parent and left siblings. This is called L-attributed SDT.
L-attributed SDT
Each attribute must either be:
- synthesized
- inherited
- For a production \(A \rightarrow X_1X_2...X_n\) with inherited attributes \(X_i.a\) computed by an
action, the rule may use only
- inherited attributes from \(A\)
- either inherited or synthesized attributes \(X_j\) for \(j < i\)
This is mostly only used with a top-down parser.
S-attributed SDT
These are used when doing bottom-up parsing. In fact, bottom-up parsing exclusively makes use of S-attributed SDTs. This is because it does not have the parent node at all. Midrule actions are basically resolved to empty non-terminals that allow the parser to treat it as a postfix SDT.
Intermediate Representation
In the syntax tree itself, we can do a lot of optimizations to have a more concise form. We can reuse subtrees for computations. As such the subgraph isomorphism problem is NP-complete.
However, we can still do it in a restricted scope. Then we number the nodes of the DAG. That gives us an evaluation ordering.
Three address code is the most common form of IR that compilers use. It has some basic forms but all of them obey one basic principle, there are no more than three variables involved.
- Static single assignments
This is later used for determining lifetime of a variable and assigning registers to them. Each definition is abstracted as a separate node. This leads to the a new register allocation for each write.
Here is where we do the register allocation optimization. Mostly heuristics and approximate algorithms are used, but even then it is an NP-hard problem.
We also introduce something called as a phi node that helps us in decision-making. It is basically an operator that lets you choose at runtime which value you want to use so that you can have an assignment for it. It is not actually there, just used for analysis.
- Types and type equivalence
With types come three questions:
- Storage requirement (size of the object)
- Storage interpretation (int or 4 chars)
- Valid operations (Add file pointer to char array data).
We say that two types are structurally equivalent iff one the following conditions is true:
- They are the same basic type (name equivalence)
- They are constructed in the same fashion from structurally equivalent types.
- One is a type name that denotes the other. (
typedef)
Name equivalence is easy to check, but it is very strict. Eg: two typedefs for int.
Structural equivalence avoids this, but then may allow nonsensical comparisons like doubly linked list node == binary search tree nodes.
Type checking involves two different techniques:
- Type synthesis: C++ templates for example. A template defines a skeleton. A type gets constructed when we define vector<int> v>; this involves type synthesis.
- Type inference: auto keyword. Function polymorphism.
A strongly typed language is one where the compiler guarantees that the valid source program will run without type errors.
- Type conversions
- Widening conversions are usually safe.
- Narrowing conversions are unsafe.
- Array expressions
For IR of array expressions, we need the type of the array to calculate the offset correctly. In case of multi-level arrays, we also need the previous size parameters to calculate that. We use row major storage, meaning that one row is together in the memory followed by the second row and so on.
- Control Flow
We mostly use short circuiting for boolean conditions so that evaluation is made easier and expensive computations are not done without a reason.
Code generation
Convert the IR to assembly
Post assembly shenanigans
First the assembler converts the assembly to an object file. Here, the addresses start with 0 and are relocatable. Later on the linker links multiple such object files together and resolves function addresses, starting location, etc. using something called as a Linker Descriptor Script.
