A net is a composition of cells and wires. A cell has arity \(n\), composed of \(n\) auxillary ports and 1 principal port. They can be taken to be inputs and outputs respectively.

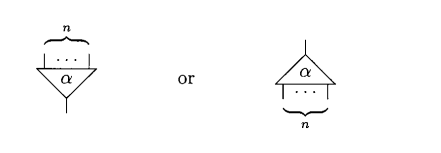
We can also have cells of arity 0.

Apart from wires and cells, we also have some free ports, which can be thought of as free variables. Cyclic wires not connecting anything are also possible.

A tree is a net \(\tau\) such that there is a distinguished free port, called the root, which can be obtained with plugging in the auxillary ports of a cell into smaller trees, or it can be a standalone wire.

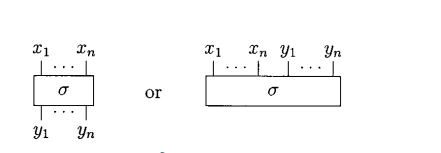
A wiring is a net without any cells and cyclic wire. A permutation is a wiring of \(n\) ports, which, represented as:

A primary reduction in the system is of this form. Fix an alphabet \(\Sigma\) with \(m\) symbols \(\alpha_1, \dots, \alpha_m\), of respective arities \(n_i\).

An interaction rule reduces two cells \(\alpha_i\) and \(\alpha_j\) are connected with their principal ports that reduces them to a wiring with \(n_i + n_j\) free ports.

Another interpretation involves exchanging the first \(n_i\) free ports with the last \(n_j\) free ports in \(v_{i,j}\).

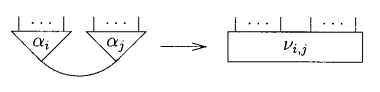
This is interpretation 1.

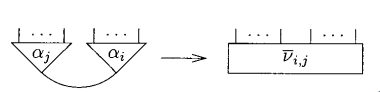
There are two restrictions to have a well defined interaction system.

• If there is a rule for \(\alpha_i\) and \(\alpha_j\), then there are no other rules for these two or the commutation of these two.
• If a symbol interacts with itself, then \(v_{i,i} = \bar{v}_{i,i}\).

We can also define a square matrix condition such that they adhere to a symmetry condition:

• If \(v_{i,j}\) is defined, then so is \(v_{j,i}\), in fact, \(v_{j,i} = \bar{v}_{{i,j}}\)

Now we prove one major and very helpful property about these nets:

If a net \(\mu\) reduces to \(\nu\) and \(\nu'\) in single steps and \(\nu \neq \nu'\), then \(\nu\) and \(\nu'\) reduce in one step to a common \(\epsilon\).

This property also guarantees that any net that reduces to an irreducible net \(e\) in \(n\) steps will always reach \(e\) in \(n\) steps.

There are two kinds of configs in a net that may lock a computation:

• irreducible cuts
• vicious cycles

A cut consists of two cells connected by their principal port. They are either reducible or irreducible. An irreducible cut can never be eliminated, because cells can only interact with their principal ports.

A vicious cycle consists of a sequence of cells whose principal port output goes into one of the auxillary ports of the next one, with the last one looping back to the first. Clearly, they cannot be eliminated, since cells only interact with their principal ports.

A reduced net is one where there are no cuts or vicious cycles. Trees and wirings are reduced and irreducible, but not every irreducible net is reduced.

From now on, any interaction system should satisfy the fact that all the right members of its reduction rules are completely reduced. If not, we cal always reduce the right members. If they're stuck, then something's wrong with the system.

Any reduced net with \(n\) free ports can be uniquely decomposed to a net of a wiring across the auxillary ports of \(n\) trees of arbitrary arities.

This is kind of obvious, since we can induct on the number of cells. If there are no cells then this is a wiring. Otherwise, pick any cell and follow the principal path, since it's a reduced net it will terminate in some cell whose principal port is free, we remove this cell and apply induction hypothesis.

A principal net is one that basically acts as a giant cell. One free principal port, and \(n\) free auxillary ports. The principal port is also called the root.

We define a translation \(\Phi\) as follows:

Let \(\Sigma\) and \(\Sigma'\) be alphabets of symbols with arities. A translation \(\Phi\) of \(\Sigma\) and \(\Sigma'\) maps each symbol \(\alpha\) of arity \(n\) in \(\Sigma\) to a principal net \(\Phi(\alpha)\) of arity \(n\), built with the symbols of \(\Sigma'\).

If the mapping is not degenerate (has more than just a single wire) for every symbol, then it is called strict.

There is a correspondence of reduced nets from the input to the output for a translation. Basically, if the input net is reduced, the translated net is also reduced. Converse holds if the translation is strict.

There are a total of 6 rules:

\(\epsilon\epsilon\) basically clears it self on its own.

\(\gamma\gamma\) and \(\delta\delta\) basically turn their auxillary ports into a pair of wires. The first one inverts while the second one retains itself.

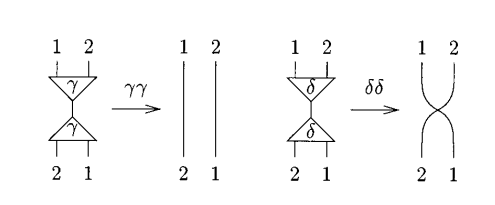
Now come the heterogenous interaction rules:

• the empty with any cell turns that cell's auxillary port into all emptys and removes the cell.
• Say a \(\delta\) is interacting with the port of another cell. Then the cell is doubled. All the arguments of the original cell are passed through the principal port of \(\delta\) and the first ones go to the first new cell and the second ones go to the second new cell.

We view them as reversible two-stack machines. Let \(\nu\) be a net of combinators that reduces to a wiring. It is possible to compute the wiring without reducing the net by simply traversing the net. We carry the two stacks (one for the two types of cells) where each element in the stack is a string over the alphabet \(\{p, q\}\). Entering through the auxillary port pushes the letter onto the stack. Entering from the principal port pops p or q from the relevant stack. If the stack becomes empty, one stops.

Obvious facts like unique execution follow. Also, a net reduced to another still has the same execution. Another definition that follows is one of equivalence. This is in terms of the free ports and the executions on those ports.

There are a total of 6 rules:

$ε